前言
谈到生活中经常坐的公交车,比较常见的算法问题可能是寻找“耗时最少公交路线”、“最少换乘公交路线”、“最便宜公交路线”、“综合最优公交路线”等。这些算法由于在地图软件中经常被使用,已经被大家研究得非常透彻,比如 Dijkstra 算法就可以用来计算“最短距离公交路线”。如想了解更多,可以阅读参考资料 2 给出的中文文献。
相比这些常见的算法问题,不如让我们来一起看看不大被人提及的“公交计费问题”。笔者经常在下雨的时候乘坐公交车,每次上车前会先取一张票,然后下车前可以看屏幕显示来知道票价。于是笔者就有了一个小问题:票价是如何正确显示的,是否可以对其建模并写个小程序模拟一下。
问题描述
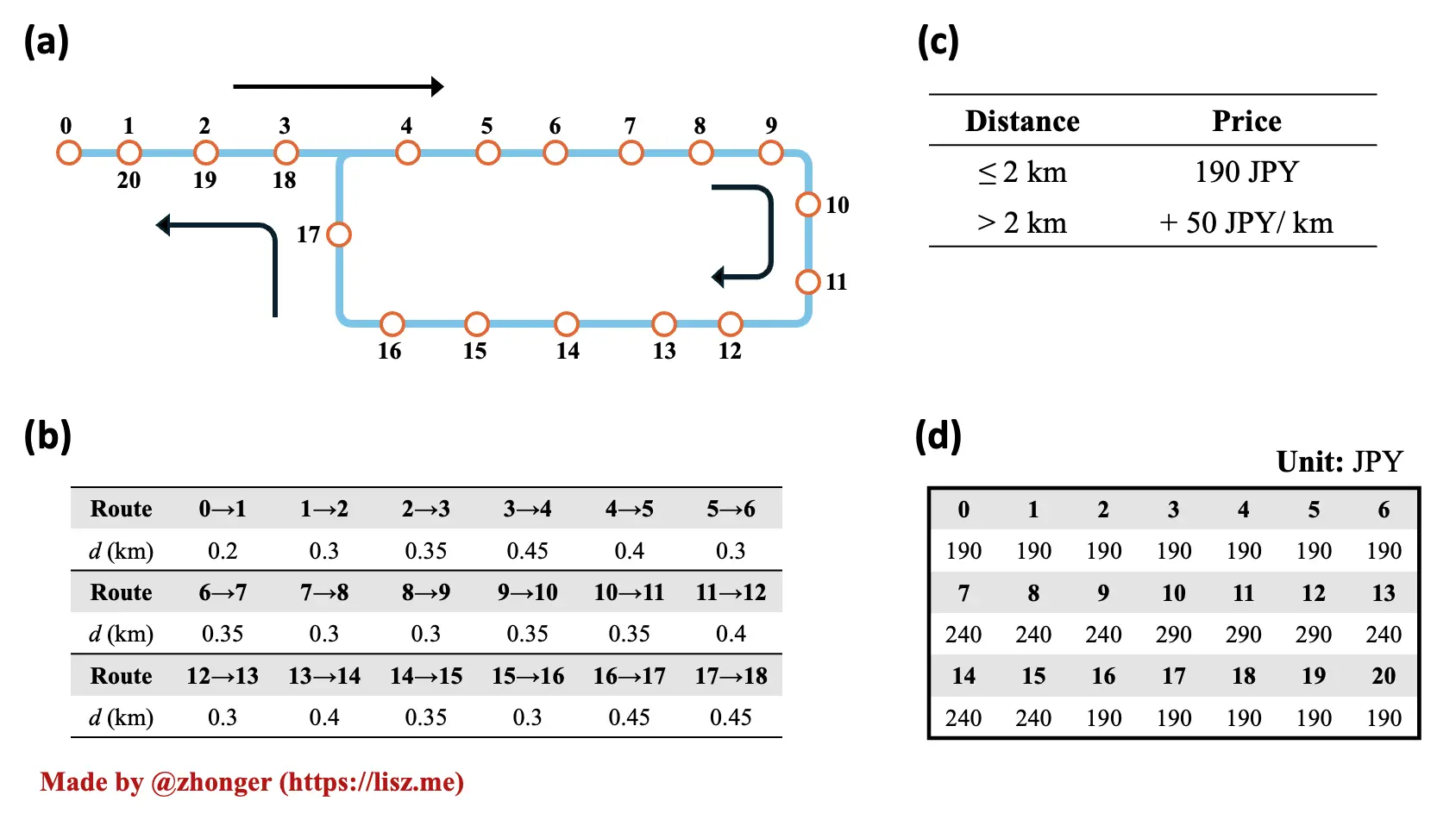
如图 1 所示为公交计费问题描述。
- (a) 公交路线图(图中为右循环路线,但对应的左循环路线也存在),0~20 为站点编号,且 1~3 与 20~18 分别对应相同。公交从站点 0 出发,按照箭头所指的方向依次行进,最终回到站点 0 并停止运行。
- (b) 相邻站点间距离,以 km 为距离计算单位,给出的数值为公交在站点间实际行进距离。
- (c) 公交票价计算方式,距离不足 2 km 为基本票价 190 日元,超过 2 km 的话每超过 1 km 加收 50 日元,如不足 1 km 按照 1 km 计算。注意,此处的距离为循环线路中上车站点与下车站点的有效距离,即站点间在循环线路上的最短距离而非实际运行距离。比如,即使从站点 0 上车,经过一圈循环后再从站点 0 下车,也只能收取基本票价 190 日元,因为有效距离为 0 km。(以上计算方式参考自资料 3)
- (d) 公交最后返回起始站点时计费状态,灰底色为站点编号,白底色为票价。
问题目标
- 打印欢迎消息,提示是否从站点 0 发车;
- 发车后,通过回车或其他操作在下一站点停车,打印当前票价状态,尚未抵达站点票价为空;
- 经过循环后回到站点 0,通过回车或其他操作停车,打印当前票价状态,如图 1(d) 所示。
解决方案
问题分析
解决公交计费问题,首先要将图 1 中给出的信息进行集成,可得如下图 2。其中,站点间的橙色数字为相邻站点间距离,红色数字为几个关键(0~2 km,2~3 km 和 3~4 km 的阈值站点)站点与出发站点 0 之间的有效距离。
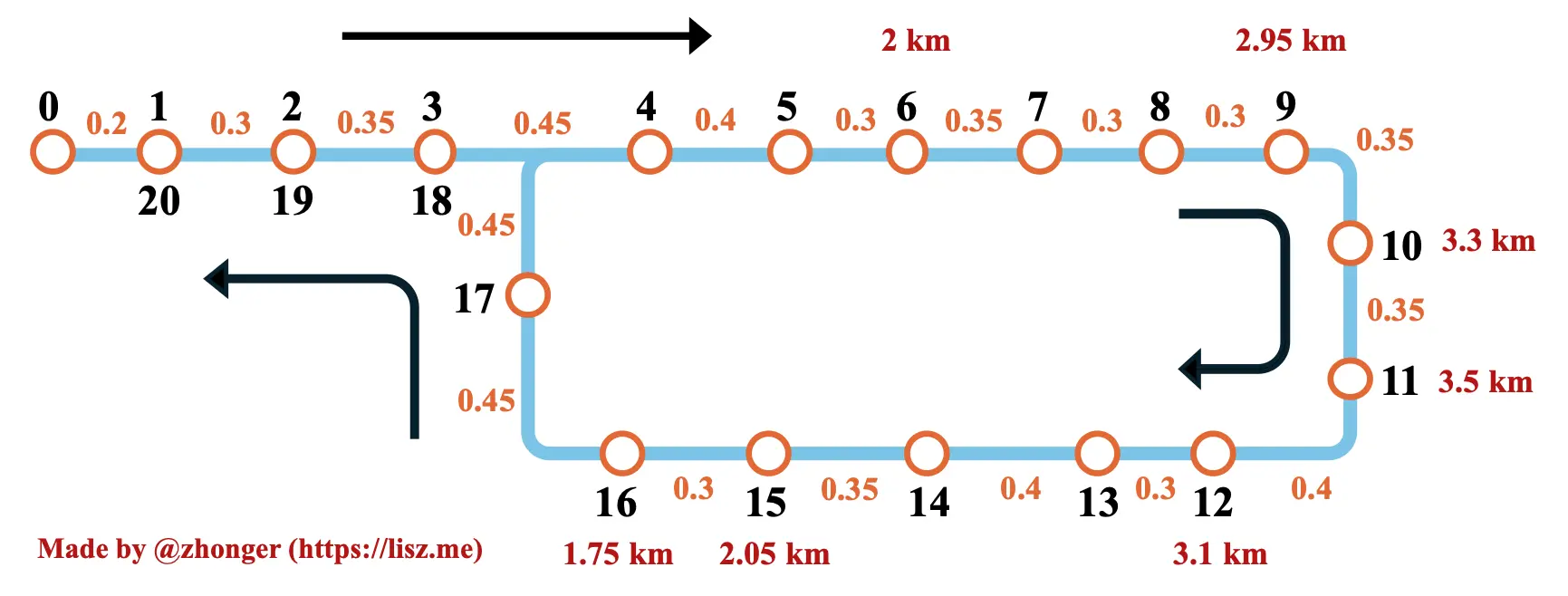
其实整个问题的核心就在于对有效距离的理解。从题干可知,有效距离并非是实际行进距离。这主要是因为给出的公交路线是环线而非直线,即出发站点与结束站点为同一站点。除此之外,刚开始的 1~3 与最后的 20~18 三个站点是重合的。根据给出的例子解释,我们可以将这里的“有效距离”粗略定义为“上车站点与下车站点在公交路线上正反距离的最小值”。我们不妨从以下示例中进一步加深对于“有效距离”的理解:(~ 表示“大约”)
- 例 1:上车站点为站点 3,下车站点为站点 17。因为站点 3 与站点 18 重合,所以有效距离等同于站点 17 和 18 之间的距离 0.45 km。
- 例 2:上车站点为站点 5,下车站点为站点 18。如例 1 方式计算可得有效距离为 0.85 km。
- 例 3:上车站点为站点 4,下车站点为站点 17。虽然按照路线实际行进距离很远,但是实际两站之间路线上最短距离大约为 0.45 km,即有效距离为 ~0.45 km。
- 例 4:上车站点为站点 5,下车站点为站点 15。如例 2 方式计算可得有效距离为 ~1.6 km。
- 例 5:上车站点为站点 6,下车站点为站点 14。按照图中方向实际行进距离计算,可知正向距离为 2.75 km,按照路线上最短反向距离为 ~2.25 km,因此有效距离为 ~2.25 km。
得出总结:
- 从例 1、2 可以看出,当上车站点和下车站点分别在重合直线和循环圈上时,位于重合直线上的站点需要注意切换到对应站点进行双重计算正反向距离,从而得到正确的有效距离。
- 从例 3~5 可以看出,当上车站点和下车站点均在循环圈上时,计算反向距离不涉及直线站点(即跨过出发站点 0)。即使站点 17 到站点 4 的实际行进路线不存在,也需以站点 17 到站点 4 闭合的循环圈来进行计算反向距离。
题干中给出信息“公交从站点 0 出发最终回到站点 0 并停止运行”,鉴于任何跨过出发站点 0 计算的距离实际上只可能由两辆公交车完成,不可能出现在一辆公交的票价计算方式中,当只在循环圈上的站点上下车时应该不考虑直线上的站点(0~3、18~20)。
说句题外话,如例 3~5 所示,可能直接走过去还更快更方便,而非坐这趟公交。
算法描述
变量声明
| 变量名 | 变量类型 | 描述 |
|---|---|---|
| distances | list | 站点列表,[0, 0.2, 0.3, …] |
| currentStop | int | 当前站点编号,0 |
| lineStops | list | 直线站点,[1, 2, 3, 18, 19, 20] |
| circleStops | list | 循环圈站点,[4, 5, …, 17] |
| ticketBase | float | 基础票价,190.00 |
| ticketStep | float | 票价梯度,50.00 |
| ticketUnit | str | 票价单位,JPY |
| baseDistance | float | 基础距离,2.00 |
| stepDistance | float | 基础距离,1.00 |
| distanceUnit | str | 距离单位,km |
| validDistances | list | 有效距离,长度为 21,默认值为 None |
| prices | list | 票价,长度为 21,默认值为 None |
| validStops | list | 有效站点,经过站点时将编号添加到列表里,默认为 [0] |
步骤描述
程序整体步骤:
- 初始化变量,当前站点编号为 0,询问是否启动;接受到启动指令(回车)后开始行进(提示)。
- 遇到停车指令(回车)后,切换站点编号为下一站点(+1),添加站点编号到 validStops。
- 循环计算 validStops 中各站点的有效距离 validDistances(具体见下)。
- 循环计算各站点的票价同时更新 prices。
- 打印计费矩阵。
- 接受到启动指令(回车)后继续行进(提示),重复 2~5 步骤直至重新回到站点 0。
- 打印到达终点站提示信息,结束程序。
计算任意两个上下车站点间的有效距离的步骤:
- 已知上车站点 a 和下车站点 b,当两站点相同时有效距离为 0,如不同进入下一步骤。
- 利用 lineStops 和 circleStops 两个变量判断 a 和 b 位于直线部分或循环圈部分。
- 如果两站点都是直线部分,利用对称方式标准化为 1~3 的站点编号,直接计算之间距离为有效距离。
- 如果两站点都是循环圈部分,利用 circleStops 进行循环遍历叠加计算正反距离,取较小的值为有效距离。
- 如果一站点在直线部分、一站点在循环圈部分,对直线部分的站点(标准化后的 1~3 站点)计算正反距离,取较小的值为有效距离。
- 返回有效距离。
程序模拟
根据以上思路,笔者采用 Python 实现了解决方案。源代码请见 Github Gist。以下为程序模拟运行效果:
结语
虽然现有的公交线路大部分还是很规则的,不同时存在循环圈和直线的情况,计费也较为简单,但是思考特殊公交线路的计费方式也不失为一件有趣的事情。上面给出的分析和算法描述,也可以用其他编程语言实现,比如用前端编程语言就可以直接可视化整个公交计费过程。
参考资料
版权声明: 如无特别声明,本文版权归 仲儿的自留地 所有,转载请注明本文链接。
(采用 CC BY-NC-SA 4.0 许可协议进行授权)
本文标题:《 生活中的小问题——公交计费问题 》
本文链接:https://lisz.me/tech/algorithm/bus-ticket.html
本文最后一次更新为 天前,文章中的某些内容可能已过时!


